Gravitational Potential and Potential Energy

The escape velocity for a planet is $V_e$. A tunnel is dug along a diameter of the planet and a small body is dropped into it at the surface. When the body reaches the centre of the planet, its speed will be

Two planets A and B have the same material density. If the radius of A is twice that of B, then the ratio of the escape velocity  $\frac{{\text{V}}_{\text{A}}}{{\text{V}}_{\text{B}}}\text{is}$

Find the work done to bring four particles each of mass $100 \mathrm{g}$ from large distances to the four vertices of a square of side $20 \mathrm{cm}$. Also, find the gravitational potential at the centre.

What is the acceleration due to gravity at a distance $3r$ from the centre of the earth if the gravitational potential at a distance $r$ from the centre of the earth is $v$? [assume$r>R$, where $R=\mathrm{radius} \mathrm{of} \mathrm{earth}$]

If the potential due to sphere at infinity is $\frac{GM}{R}$. Then, gravitational potential at the centre of a uniform solid sphere of mass $M$ and radius $R$ is _____.

Two identical containers $X$ and $Y$ are connected at the bottom by a thin tube of negligible volume. The tube has a valve in it, as shown in the figure. Initially container $X$ has a liquid filled up to height $h$ in it and container $Y$ is empty. When the valve is opened, both containers have equal amount of liquid in equilibrium. If the initial (before the valve is opened) potential energy of the liquid is $P_1$ and the final potential energy is $P_2$ then:

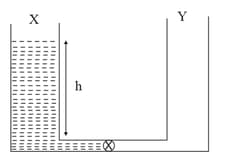
Two bodies of mass $m$ and $9m$ are placed at a distance $R$. The gravitational potential on the line joining the bodies where the gravitational field equals zero, will be ($G=$gravitational constant):

Given below are two statements:
Statement I : For a planet, if the ratio of mass of the planet to its radius increase, the escape velocity from the planet also increase.

Statement II : Escape velocity is independent of the radius of the planet.

In the light of above statements, choose the most appropriate answer from the options given below

The ratio of escape velocity of a planet to the escape velocity of earth will be:-

Given: Mass of the planet is $16$ times mass of earth and radius of the planet is $4$ times the radius of earth.

A planet having mass $9 {\mathrm{M}}_{\mathrm{e}}$ and radius $4{\mathrm{R}}_{\mathrm{e}},$ where ${\mathrm{M}}_{\mathrm{e}}$ and ${\mathrm{R}}_{\mathrm{e}}$ are mass and radius of earth respectively, has escape velocity in $\mathrm{km} {\mathrm{s}}^{-1}$ given by: (Given escape velocity on earth $V_{\mathrm{e}}=11.2\times {10}^3 \mathrm{m} {\mathrm{s}}^{-1}$)

A body is released from a height equal to the radius $\left(R\right)$ of the earth. The velocity of the body when it strikes the surface of the earth will be: (Given $g=$ acceleration due to gravity on the earth.)

A space ship of mass $2\times {10}^4 \mathrm{kg}$ is launched into a circular orbit close to the earth surface. The additional velocity to be imparted to the space ship in the orbit to overcome the gravitational pull will be (if $g=10 \mathrm{m} {\mathrm{s}}^{-2}$ and radius of earth $=6400 \mathrm{km}$ ):

Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.

Assertion A: Earth has atmosphere whereas moon doesn’t have any atmosphere.

Reason R: The escape velocity on moon is very small as compared to that on earth.

In the light of the above statements, choose the correct answer from the options given below:

A particle is released from a height equal to radius of Earth $\left(R\right)$. Find its velocity when it strikes the ground.

If a planet has mass equal to $16$ times the mass of earth, and radius equal to $4$ times that of earth. The ratio of escape speed of planet to that of earth is

If earth has a mass nine times and radius twice to that of a planet$P$. Then $\frac{v_e}{3}\sqrt{x} \mathrm{m} {\mathrm{s}}^{-1}$ be the minimum velocity required by a rocket to pull out of gravitational force of$P$, the value of $x$ is

Assuming that the gravitational potential energy of an object at infinity is zero, the change in potential energy (final - initial) of an object of mass $m$, when taken to a height $h$ from the the surface of earth (of radius $R$), is given by,

 A particle is fired vertically upward with a speed of $9.8 \mathrm{km} {\mathrm{s}}^{-1}$. Find the maximum height attained by the particle. Radius of earth = $6400 \mathrm{km}$ and $\mathrm{g}$at the surface is $9.8 \mathrm{m} {\mathrm{s}}^{-2}$. Consider only earth's gravitation.
 

Given that the gravitation potential on Earth surface is $V_0$. The potential at a point distant half the radius of earth from the centre will be

The gravitational potential energy of a system of three particles of mass $m$ each kept at the vertices of equilateral triangle of side $x$ will be